上海华师大二附中高中一年级(上)12月月考数学试题
1、填空题
1.已知2a=3,log35=b,则log1520=__________(用a,b表示)
2.已知lg(x﹣y)+lg(x+2y)=lg2+lgx+lgy,则![]() =__________.
=__________.
3.已知a,b∈R,命题p:![]() ,命题q:|a+b|=|a|+|b|,则p是q成立的__________条件.
,命题q:|a+b|=|a|+|b|,则p是q成立的__________条件.
4.函数![]() 的单调递增区间是:__________.
的单调递增区间是:__________.
5.借用计算器用二分法求方程2x+3x=7的近似解x0=__________(精准到0.01)
6.设x∈R,[x]表示不大于x的最大整数,如![]() ,则使[|x﹣1|]=3成立的x的取值范围__________.
,则使[|x﹣1|]=3成立的x的取值范围__________.
7.函数f(x)=﹣x2+2x的概念域和值域分别是[m,n]和[3m,3n],则m+n=__________.
8.已知函数f(x)=![]() 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有![]() <0成立,则a的取值范围是__________.
<0成立,则a的取值范围是__________.
9.已知函数y=f(x)和y=g(x)在[﹣2,2]的图象如,给出下列四个命题:
(1)方程f[g(x)]=0有且仅有6个根
(2)方程g[f(x)]=0有且仅有3个根
(3)方程f[f(x)]=0有且仅有5个根
(4)方程g[g(x)]=0有且仅有4个根
其中正确命题是__________.

10.设x,y为实数,且满足![]() ,则x+y=__________.
,则x+y=__________.
11.不等式(x+1)(x2﹣4x+3)>0有多种解法,其中有一种办法如下,在同一直角坐标系中作出y1=x+1和y2=x2﹣4x+3的图象然后进行求解,请类比求解以下问题:
设a,b∈Z,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则a+b=__________.
12.已知函数![]() 若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是__________.
若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是__________.
2、选择题
13.由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的需要出发,用有理数的“分割”来概念无理数(史称戴德金分割),并把实数理论打造在严格的科学基础上,才结束了无理数被觉得“无理”的年代,也结束了持续2000多年的数学史上的首次大危机.所谓戴德金分割,是指或有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每个元素都小于N中的每个元素,则称(M,N)为戴德金分割试判断,对于任一戴德金分割(M,N),下列选项中,不可能成 立的是()
A.M没最大元素,N有一个最小元素
B.M没最大元素,N也没最小元素
C.M有一个最大元素,N有一个最小元素
D.M有一个最大元素,N没最小元素
14.若函数f(x)对任意x,y∈R满足f(x+y)+f(x﹣y)=2f(x)f(y),则下列关于函数奇偶性的说法肯定正确的是()
A.是偶函数但不是奇函数
B.是奇函数但不是偶函数
C.是非奇非偶函数
D.可能是奇函数也会是偶函数
15.在同一坐标系中,函数y=ax+1与y=a|x﹣1|(a>0且a≠1)的图象可能是()
A. B.
B. C.
C. D.
D.
16.如图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当P沿着A﹣B﹣C﹣M运动时,以点P经过的路程x为自变量,三角形APM的面积为y,函数y=f(x)的图象大致是()
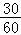
A.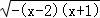 B.
B.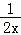 C.
C.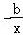 D.
D.
3、解答卷
17.已知关于x的方程k•9x﹣3k•3x+6(k﹣5)=0,x∈[0,2];分别求满足下列条件的实数k的取值范围:(1)有解;(2)有唯一解;(3)有两个解.
18.在一次水下考古活动中,潜水员需潜入水深为30米的水底进行作业.其用氧量包括以下三个方面:①下潜时,平均速度为每分钟x米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为y升.
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为y升.
(1)将y表示为x的函数;
(1)若x∈[4,8],求总用氧量y的取值范围.
19.已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y)且当x>0,f(x)<0,且f(1)=﹣2.
(1)判断f(x)的奇偶性;
(2)求f(x)在区间[﹣3,3]上的最大值;
(3)解关于x的不等式f(ax2)﹣2f(x)<f(ax)+4.
20.概念符号函数sgn(x)=![]() ,已知a,b∈R,f(x)=x|x﹣a|sgn(x﹣1)+b.
,已知a,b∈R,f(x)=x|x﹣a|sgn(x﹣1)+b.
(1)求f(2)﹣f(1)关于a的表达式,并求f(2)﹣f(1)的最小值.
(2)当b=![]() 时,函数f(x)在(0,1)上有唯一零点,求a的取值范围.
时,函数f(x)在(0,1)上有唯一零点,求a的取值范围.
(3)已知存在a,使得f(x)<0对任意的x∈[1,2]恒成立,求b的取值范围.
2017-2018学年上海华师大二附中高中一年级(上)12月月考数学试题
参考答案与考试试题分析
1、填空题
1.已知2a=3,log35=b,则log1520=__________![]() __________(用a,b表示)
__________(用a,b表示)
【考试知识点】对数的运算性质.
【剖析】2a=3,可得a=log23=![]() ,又log35=b=
,又log35=b=![]() ,可得lg3=alg2,lg5=blg3=balg2.代入log1520=
,可得lg3=alg2,lg5=blg3=balg2.代入log1520=![]() 即可得出.
即可得出.
【解答】解:∵2a=3,∴a=log23=![]() ,又log35=b=
,又log35=b=![]() ,
,
∴lg3=alg2,lg5=blg3=balg2.
则log1520=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
2.已知lg(x﹣y)+lg(x+2y)=lg2+lgx+lgy,则![]() =__________.
=__________.
【考试知识点】对数的运算性质.
【剖析】依据对数运算知,lg[(x﹣y)(x+2y)]=lg(2xy),即(x﹣y)(x+2y)=2xy,又由于x>0,y>0进而得到答案.
【解答】解:∵lg(x﹣y)+lg(x+2y)=lg[(x﹣y)(x+2y)]
lg2+lgx+lgy=lg(2xy)
∴(x﹣y)(x+2y)=2xy
∴(x﹣2y)(x+y)=0
又∵x>0,y>0
∴x=2y,∴![]() =2
=2
故答案为:2.
3.已知a,b∈R,命题p:![]() ,命题q:|a+b|=|a|+|b|,则p是q成立的__________条件.
,命题q:|a+b|=|a|+|b|,则p是q成立的__________条件.
【考试知识点】必要条件、充分条件与充要条件的判断.
【剖析】大家可以参考充要条件的概念进行判断,但解题的重点是绝对值不等式及不等式的性质应用
【解答】解:命题p:由![]() ,可得a<0,b≤0,或a≤0,b<0,
,可得a<0,b≤0,或a≤0,b<0,
命题q:|a+b|=|a|+|b|,可得ab≥0,
故p⇒q,但q推不出p,
故p是q成立的充分非必要,
故答案为:充分非必要
4.函数![]() 的单调递增区间是:__________
的单调递增区间是:__________![]() __________.
__________.
【考试知识点】指数函数的单调性与特殊点.
【剖析】令t=![]() ,则 y=
,则 y=![]() ,函数 y的增区间就是t的减区间,问题转化为求t的减区间.
,函数 y的增区间就是t的减区间,问题转化为求t的减区间.
【解答】解:令t=![]() =
=![]() =
=![]() ,
,
∴y=![]() ,
,![]() ≥t≥0,﹣1≤x≤2,
≥t≥0,﹣1≤x≤2,
故t的减区间为[![]() ,2],
,2],
∴函数 y的增区间为[![]() ,2].
,2].
5.借用计算器用二分法求方程2x+3x=7的近似解x0=__________(精准到0.01)
【考试知识点】二分法求方程的近似解.
【剖析】方程的近似解所在的区间即是函数f(x)=2x+3x﹣7的一个零点所在的区间,此区间应满足:①区间长度小于精度0.01,②区间端点的函数值的符号相反.
【解答】解:令f(x)=2x+3x﹣7,
∵f(1)=2+3﹣7<0,f(2)=4+6﹣7>0,
∴f(x)=0的解在区间(1,2)上,
区 间 | 中点值 | 中点函数值 |
(1,2) | 1.5 | 0.328427 |
(1,1.5) | 1.25 | ﹣0.87159 |
(1.25,1.5) | 1.375 | ﹣0.28132 |
(1.375,1.5) | 1.4375 | 0.021011 |
(1.375,1.435) | 1.405 | ﹣0.136822 |
| 1.42 | ﹣0.064145 |
(1.42,1.435) | 1.4275 | ﹣0.001769 |
(1.4275,1.435) | 1.43125 | ﹣0.009447 |
∴f(x)=0的解在区间(1.43125,1435)上,
二分法求方程2x+3x=7的近似解x0=1.43
故答案为:
1.43
6.设x∈R,[x]表示不大于x的最大整数,如![]() ,则使[|x﹣1|]=3成立的x的取值范围______________________________.
,则使[|x﹣1|]=3成立的x的取值范围______________________________.
【考试知识点】函数的概念域及其求法.
【剖析】由题意,依据所给的概念可将[|x﹣1|]=3转化为3≤|x﹣1|<4,解此绝对值不等式即可求出x的取值范围
【解答】解:由题意[|x﹣1|]=3,则3≤|x﹣1|<4
∴3≤x﹣1<4或﹣4≤x﹣1<﹣3
解得4≤x<5或﹣3<x≤﹣2
所以使[|x﹣1|]=3成立的x的取值范围是(﹣3,﹣2]∪[4,5)
故答案为(﹣3,﹣2]∪[4,5)
7.函数f(x)=﹣x2+2x的概念域和值域分别是[m,n]和[3m,3n],则m+n=__________.
【考试知识点】二次函数的性质.
【剖析】由题意可得,函数在区间[m,n]上为增函数,则![]() ,解得即可.
,解得即可.
【解答】解:函数f(x)=﹣x2+2x的对称轴方程式x=1,
由题意可得,函数在区间[m,n]上为增函数,则![]() ,
,
则m,n时方程﹣x2+2x=3x的两个根,
∴m+n=﹣1,
故答案为:﹣1
8.已知函数f(x)=![]() 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有![]() <0成立,则a的取值范围是__________
<0成立,则a的取值范围是__________![]() ____________________.
____________________.
【考试知识点】函数单调性的判断与证明.
【剖析】依据已知条件可知函数f(x)在R上单调递减,所以对于ax,0<a<1;对于(a﹣3)x+4a,a<3,又ax>1,所以(a﹣3)x+4a的最大值满足小于等于1,而(a﹣3)x+4a对于x≥0时的最大值为4a,所以4a≤1,所以得到![]() ,和前面的0<a<1的a的取值求交集即得a的取值范围.
,和前面的0<a<1的a的取值求交集即得a的取值范围.
【解答】解:∵对任意x1≠x2,都有![]() <0成立;
<0成立;
∴f(x1)﹣f(x2)与x1﹣x2异号,
即x1﹣x2<0时,f(x1)﹣f(x2)>0,即x1<x2时,f(x1)>f(x2);
∴函数f(x)在R上是减函数;
∴x<0时,f(x)=ax,0<a<1;
x≥0时,f(x)=(a﹣3)x+4a,a﹣3<0,a<3,又ax>1,(a﹣3)x+4a)max=4a≤1,
∴![]() ;
;
又0<a<1,∴0<a≤![]() ;
;
∴a的取值范围是![]() .
.
故答案为:![]() .
.
9.已知函数y=f(x)和y=g(x)在[﹣2,2]的图象如,给出下列四个命题:
(1)方程f[g(x)]=0有且仅有6个根
(2)方程g[f(x)]=0有且仅有3个根
(3)方程f[f(x)]=0有且仅有5个根
(4)方程g[g(x)]=0有且仅有4个根
其中正确命题是__________.

【考试知识点】函数与方程的综合运用;根的存在性及根的个数判断.
【剖析】把复合函数的概念域和值域进行对接,看满足外层函数为零时内层函数有几个自变量与之相对应.
【解答】解:∵在y为[﹣2,﹣1]时,g(x)有两个自变量满足,在y=0,y为[1,2]时,g(x)同样都是两个自变量满足
∴(1)正确
∵f(x)值域在[﹣1,2]上都是一一对应,而在值域[0,1]上都对应3个原像,
∴(2)错误
同理可知(3)(4)正确.
故答案为:(1)(3)(4).
10.设x,y为实数,且满足![]() ,则x+y=__________.
,则x+y=__________.
【考试知识点】有理数指数幂的化简求值.
【剖析】设f(t)=t2017+2013t+1,依据导数判断函数的单调性,即可得到x﹣1=1﹣y,则x+y=2,问题得以解决.
【解答】解:方程组可化为![]()
设f(t)=t2017+2013t+1,
则f′(t)=2017t2016+2013>0,
所以(t)=t2017+2013t+1为单调递增函数,
所以x﹣1=1﹣y,
则x+y=2,
故答案为:2
11.不等式(x+1)(x2﹣4x+3)>0有多种解法,其中有一种办法如下,在同一直角坐标系中作出y1=x+1和y2=x2﹣4x+3的图象然后进行求解,请类比求解以下问题:
设a,b∈Z,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则a+b=__________.
【考试知识点】类比推理.
【剖析】若对任意x≤0,都有(ax+2)(x2+2b)≤0,则y1=ax+2应为增函数,y2=x2+2b的图象顶点应在x轴下方,且函数与x负半轴交于同一点,结合a,b∈Z,可得答案.
【解答】解:类比图象法解不等式的办法,在同一坐标系中,画出y1=ax+2和y2=x2+2b的图象,
若对任意x≤0,都有(ax+2)(x2+2b)≤0,则两个函数图象应如下图所示:
则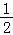 ,
,
由a,b∈Z得:![]() ,
,
∴a+b=﹣1,
故答案为:﹣1

12.已知函数![]() 若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是______________________________.
若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是______________________________.
【考试知识点】函数与方程的综合运用;分段函数的分析式求法及其图象的作法.
【剖析】由题知f(x)为分段函数,当x大于0时,由f(x)=f(x﹣1)可知当x大于1时,f(x)=0,小于1大于0时函数为减函数;当x小于等于0时函数为减函数,而方程f(x)=x+a有且只有两个不相等的实数根即f(x)与y=x+a由两个交点,在同一坐标系中画出函数f(x)的图象与函数y=x+a的图象,借助数形结合,易求出满足条件实数a的取值范围.
【解答】解:函数f(x)=![]() 的图象如图所示,
的图象如图所示,
当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,
即方程f(x)=x+a有且只有两个不相等的实数根.
故答案为(﹣∞,1)

2、选择题
13.由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的需要出发,用有理数的“分割”来概念无理数(史称戴德金分割),并把实数理论打造在严格的科学基础上,才结束了无理数被觉得“无理”的年代,也结束了持续2000多年的数学史上的首次大危机.所谓戴德金分割,是指或有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每个元素都小于N中的每个元素,则称(M,N)为戴德金分割试判断,对于任一戴德金分割(M,N),下列选项中,不可能成 立的是()
A.M没最大元素,N有一个最小元素
B.M没最大元素,N也没最小元素
C.M有一个最大元素,N有一个最小元素
D.M有一个最大元素,N没最小元素
【考试知识点】集合的表示法.
【剖析】由题意依次举例对四个命题判断,从而确定答案.
【解答】解:若M={x∈Q|x<0},N={x∈Q|x≥0};则M没最大元素,N有一个最小元素0;故A正确;
若M={x∈Q|x<![]() },N={x∈Q|x≥
},N={x∈Q|x≥![]() };则M没最大元素,N也没最小元素;故B正确;
};则M没最大元素,N也没最小元素;故B正确;
M有一个最大元素,N有一个最小元素不可能,故C不正确;
若M={x∈Q|x≤0},N={x∈Q|x>0};M有一个最大元素,N没最小元素,故D正确;
故选C.
14.若函数f(x)对任意x,y∈R满足f(x+y)+f(x﹣y)=2f(x)f(y),则下列关于函数奇偶性的说法肯定正确的是()
A.是偶函数但不是奇函数
B.是奇函数但不是偶函数
C.是非奇非偶函数
D.可能是奇函数也会是偶函数
【考试知识点】抽象函数及其应用.
【剖析】在抽象表达式中令x=y=0代入表达式,再分类讨论在抽象表达式中令x=0,y不动,结合(1)的结论即可获得f(﹣y)与f(y)之间的关系,从而获得函数的奇偶性.
【解答】解:令x=y=0则有f(0)+f(0)=2f(0)f(0),
则2f(0)=f(0)f(0),
当f(0)=0时,再令x=0
则有f(y)+f(﹣y)=2f(0)f(y)=0
所以f(﹣y)=﹣f(y),
所以y=f(x)是奇函数.
当f(0)≠0,则f(0)=1.
再令x=0
则有f(y)+f(﹣y)=2f(0)f(y),
所以f(﹣y)=f(y),
所以y=f(x)是偶函数.
故选:D
15.在同一坐标系中,函数y=ax+1与y=a|x﹣1|(a>0且a≠1)的图象可能是()
A. B.
B. C.
C. D.
D.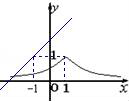
【考试知识点】指数函数的图象变换.
【剖析】当a>1时,直线y=ax+1的斜率大于1,函数y=a|x﹣1|(a>0且a≠1)在(1,+∞)上是增函数;当1>a>0时,直线y=ax+1的斜率大于0且小于1,函数y=a|x﹣1|(a>0且a≠1)在
(1,+∞)上是减函数,结合图象得出结论.
【解答】解:当a>1时,直线y=ax+1的斜率大于1,函数y=a|x﹣1|(a>0且a≠1)在(1,+∞)上是增函数,选项C满足条件.
当1>a>0时,直线y=ax+1的斜率大于0且小于1,函数y=a|x﹣1|(a>0且a≠1)在(1,+∞)上是减函数,没选项满足条件.
故选C.
16.如图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当P沿着A﹣B﹣C﹣M运动时,以点P经过的路程x为自变量,三角形APM的面积为y,函数y=f(x)的图象大致是()

A.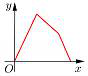 B.
B. C.
C. D.
D.
【考试知识点】函数的图象.
【剖析】当点在AB上移动时、当点在BC上移动时、当点在CD上时,讨论y随x的变化关
【解答】解:依据题意和图形可知:点P按A⇒B⇒C⇒M的顺序在边长为1的正方形边上运动,△APM的面积分为3段;
当点在AB上移动时,高不变底边渐渐变大,故面积渐渐变大;
当点在BC上移动时,y=S正方形﹣S△ADM﹣S△ABP﹣S△PCM
=1﹣![]() ﹣
﹣![]() ×1×(x﹣1)﹣
×1×(x﹣1)﹣![]() ×
×![]() ×(2﹣x)=﹣
×(2﹣x)=﹣![]() x+
x+![]() ,此函数是关于x的递减函数;
,此函数是关于x的递减函数;
当点在CD上时,高不变,底边变小故面积愈加小直到0为止.
故选:A.
3、解答卷
17.已知关于x的方程k•9x﹣3k•3x+6(k﹣5)=0,x∈[0,2];分别求满足下列条件的实数k的取值范围:(1)有解;(2)有唯一解;(3)有两个解.
【考试知识点】函数与方程的综合运用;根的存在性及根的个数判断.
【剖析】(1)设t=3x,由指数函数的单调性,可得t的范围,将方程化为k=![]() 在[1,9]有解,设f(t)=t2﹣3t+6,求出在[1,9]的值域,即可得到所求k的范围.
在[1,9]有解,设f(t)=t2﹣3t+6,求出在[1,9]的值域,即可得到所求k的范围.
(2)借助(1)的结果,通过函数的单调性与函数图象,求解方程只有一个解时k的范围;
(3)借助函数的图象,写出由两个解时k的范围.
【解答】解:(1)设t=3x,由x∈[0,2],可得t∈[1,9],
方程k•9x﹣k•3x+1+6(k﹣5)=0,即为kt2﹣3kt+6(k﹣5)=0,
即k=![]() 在[1,9]有解,
在[1,9]有解,
由f(t)=t2﹣3t+6=(t﹣![]() )2+
)2+![]() ,
,
当t=![]() ∈[1,9]时,f(t)获得最小值
∈[1,9]时,f(t)获得最小值![]() ,
,
f(1)=4,f(9)=60,可得f(t)的最大值为60.
可得k的最小值为![]() =
=![]() ,
,
k的最大值为![]() =8,
=8,
即有k的取值范围是[![]() ,8].
,8].
(2)由(1)可知k=![]() 在[1,9]有解,
在[1,9]有解,
由f(t)=t2﹣3t+6=(t﹣![]() )2+
)2+![]() ,
,
t∈[1,![]() )f(t)是减函数,函数k是增函数;
)f(t)是减函数,函数k是增函数;
t∈(![]() ,9],f(t)是增函数,函数k是减函数.
,9],f(t)是增函数,函数k是减函数.
t=1时,k=![]() ,t=9时,k=
,t=9时,k=![]() ,函数k=
,函数k=![]() 在[1,9]的图象如图:
在[1,9]的图象如图:
有唯一解;实数k的取值范围:![]() ;
;
(3)有两个解.实数k的取值范围:![]() ;
;
18.在一次水下考古活动中,潜水员需潜入水深为30米的水底进行作业.其用氧量包括以下三个方面:①下潜时,平均速度为每分钟x米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为y升.
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为y升.
(1)将y表示为x的函数;
(1)若x∈[4,8],求总用氧量y的取值范围.
【考试知识点】函数模型的选择与应用.
【剖析】(1)通过速度、时间与路程之间的关系可知下潜所需时间为![]() 分钟、返回所需时间为
分钟、返回所需时间为![]() 分钟,进而列式可得结论;
分钟,进而列式可得结论;
(2)通过基本不等式可知及x∈[4,8]可知![]() 在[4,6]上单调递减、在[6,8]上单调递增,比较当x=4、8时的取值状况即得结论.
在[4,6]上单调递减、在[6,8]上单调递增,比较当x=4、8时的取值状况即得结论.
【解答】解:(1)依题意,下潜所需时间为![]() 分钟;返回所需时间为
分钟;返回所需时间为![]() 分钟,
分钟,
∴![]() ,
,
整理得:![]() (x>0);
(x>0);
(2)由基本不等式可知![]() ,当且仅当
,当且仅当![]() 即x=6时取等号,
即x=6时取等号,
由于x∈[4,8],
所以![]() 在[4,6]上单调递减、在[6,8]上单调递增,
在[4,6]上单调递减、在[6,8]上单调递增,
所以当x=6时,y取最小值7,
又由于当x=4时![]() ;当x=8时
;当x=8时![]() ,
,
所以y的取值范围是:![]() .
.
19.已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y)且当x>0,f(x)<0,且f(1)=﹣2.
(1)判断f(x)的奇偶性;
(2)求f(x)在区间[﹣3,3]上的最大值;
(3)解关于x的不等式f(ax2)﹣2f(x)<f(ax)+4.
【考试知识点】抽象函数及其应用;函数奇偶性的判断.
【剖析】(1)取x=y=0可得f(0)=0;再取y=﹣x代入即可;
(2)先判断函数的单调性,再求函数的最值;
(3)因为f(x)为奇函数,整理原式得 f(ax2)+f(﹣2x)<f(ax)+f(﹣2);即f(ax2﹣2x)<f(ax﹣2);再由函数的单调性可得ax2﹣2x>ax﹣2,从而求解.
【解答】解:(1)取x=y=0,
则f(0+0)=f(0)+f(0);
则f(0)=0;
取y=﹣x,则f(x﹣x)=f(x)+f(﹣x),
∴f(﹣x)=﹣f(x)对任意x∈R恒成立
∴f(x)为奇函数;
(2)任取x1,x2∈(﹣∞,+∞)且x1<x2,则x2﹣x1>0;
∴f(x2)+f(﹣x1)=f(x2﹣x1)<0;
∴f(x2)<﹣f(﹣x1),
又∵f(x)为奇函数
∴f(x1)>f(x2);
∴f(x)在(﹣∞,+∞)上是减函数;
∴对任意x∈[﹣3,3],恒有f(x)≤f(﹣3)
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=﹣2×3=﹣6;
∴f(﹣3)=﹣f(3)=6;
∴f(x)在[﹣3,3]上的最大值为6;
(3)∵f(x)为奇函数,
∴整理原式得 f(ax2)+f(﹣2x)<f(ax)+f(﹣2);
即f(ax2﹣2x)<f(ax﹣2);
而f(x)在(﹣∞,+∞)上是减函数,
∴ax2﹣2x>ax﹣2;
∴(ax﹣2)(x﹣1)>0.
∴当a=0时,x∈(﹣∞,1);
当a=2时,x∈{x|x≠1且x∈R};
当a<0时,![]() ;
;
当0<a<2时,![]()
当a>2时,![]() .
.
20.概念符号函数sgn(x)=![]() ,已知a,b∈R,f(x)=x|x﹣a|sgn(x﹣1)+b.
,已知a,b∈R,f(x)=x|x﹣a|sgn(x﹣1)+b.
(1)求f(2)﹣f(1)关于a的表达式,并求f(2)﹣f(1)的最小值.
(2)当b=![]() 时,函数f(x)在(0,1)上有唯一零点,求a的取值范围.
时,函数f(x)在(0,1)上有唯一零点,求a的取值范围.
(3)已知存在a,使得f(x)<0对任意的x∈[1,2]恒成立,求b的取值范围.
【考试知识点】分段函数的应用.
【剖析】(1)依据已知求出f(2)﹣f(1)=2|2﹣a|﹣|1﹣a|=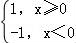 ,剖析其单调性可得函数的最小值;
,剖析其单调性可得函数的最小值;
(2)当x∈(0,1)时,f(x)=![]() ,由f(x)=0得:
,由f(x)=0得:![]() ,即
,即![]() ,令g(x)=|x﹣a|,h(x)=
,令g(x)=|x﹣a|,h(x)=![]() ,在同一坐标系中分别作出两个函数在(0,1)上的图象,数形结合可得答案;
,在同一坐标系中分别作出两个函数在(0,1)上的图象,数形结合可得答案;
(3)若存在a,使得f(x)<0对任意的x∈[1,2]恒成立,则![]() +x<a<
+x<a<![]() +x对任意的x∈[1,2]恒成立,分类讨论可得答案.
+x对任意的x∈[1,2]恒成立,分类讨论可得答案.
【解答】解:(1)∵函数sgn(x)=![]() ,f(x)=x|x﹣a|sgn(x﹣1)+b.
,f(x)=x|x﹣a|sgn(x﹣1)+b.
∴f(2)=2|2﹣a|+b,f(1)=|1﹣a|+b,
∴f(2)﹣f(1)=2|2﹣a|﹣|1﹣a|=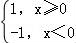 ,
,
由f(2)﹣f(1)在(﹣∞,2]上为减函数,在(2,+∞)上为增函数,
故当a=2时,f(2)﹣f(1)的最小值为﹣1;
(2)当b=![]() 时,函数f(x)=﹣x|x﹣a|+
时,函数f(x)=﹣x|x﹣a|+![]() =
= ,
,
当x∈(0,1)时,f(x)=![]() ,
,
由f(x)=0得:![]() ,即
,即![]() ,
,
令g(x)=|x﹣a|,h(x)=![]() ,
,
在同一坐标系中分别作出两个函数在(0,1)上的图象,如下图所示:

由图可得:当a∈(﹣∞,![]() )∪{
)∪{![]() }∪[
}∪[![]() ,+∞)时,两个函数图象有且只有一个交点,
,+∞)时,两个函数图象有且只有一个交点,
即函数f(x)在(0,1)上有唯一零点;
(3)x∈[1,2]时,f(x)=x|x﹣a|+b,
由f(x)<0得:|x﹣a|<![]() ,
,
∴b<0,且![]() <x﹣a<
<x﹣a<![]() 对任意的x∈[1,2]恒成立,
对任意的x∈[1,2]恒成立,
即![]() +x<a<
+x<a<![]() +x对任意的x∈[1,2]恒成立,
+x对任意的x∈[1,2]恒成立,
∵y=![]() +x在[1,2]上单调递增,故当x=2时,y=
+x在[1,2]上单调递增,故当x=2时,y=![]() +x取最大值2+
+x取最大值2+![]() ,
,
y=![]() +x,x∈[1,2]的最小值为:
+x,x∈[1,2]的最小值为: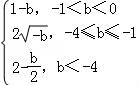 ,
,
①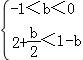 ,解得:b∈(﹣1,﹣
,解得:b∈(﹣1,﹣![]() );
);
②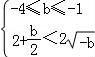 ,解得:b∈[﹣4,﹣1];
,解得:b∈[﹣4,﹣1];
③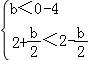 解得:b∈(﹣∞,﹣4),
解得:b∈(﹣∞,﹣4),
综上可得:b∈(﹣∞,﹣![]() ).
).







